Description
Problem 1. (pencil and paper) (0 points – do not hand in)
Determine the natural cubic spline that interpolates the function f(x) = x
6 over the interval [0,2] using knots 0, 1 and 2.
Problem 2. (computer) (0 points – do not hand in)
Write a program which determines a natural cubic spline S(x) based on a table of values
and evaluates the spline function at a given value of x. Test the code by determining the
natural cubic spline interpolant for f(x) = sin(x) + 0.04x
2
at the following 15 unevenly
spaced knots in the interval [−9.7,12.3]:
x0 ··· x4 -9.7000 -7.3000 -5.4000 -5.0000 -3.0100
x5 ··· x9 -2.1300 -1.2000 -0.5600 0.0000 1.2000
x10 ··· x14 4.5000 6.7000 9.9000 10.0000 12.3000
Evaluate the spline at 100 equally spaced points in the interval [−9.7,12.3]. Print out the
value of S(x) and also the absolute error |S(x) − f(x)|. Present your results graphically
(S(x) and f(x) vs. x and |S(x)− f(x)| vs. x).
Problem 3. (computer) (0 points – do not hand in)
Write a program to estimate f
0
(x) for any x in [a,b] assuming that we know only the
values of f(x) at knots a = t0 < t1 < ... < tn = b. Test your program using the set of data
points {x, f(x)} given in Problem 2 (use the given x values and the corresponding values
of f(x) = sin(x) +0.04x
2
).
Evaluate the derivative of the spline function S
0
(x) at 100 equally spaced points in the
interval [−9.7,12.3]. Present your results graphically in a plot showing S
0
(x) and f
0
(x) =
cos(x) +0.08x as a function of x.
Problem 4. (2 points)
(a) (computer) Use your programs developed in Problems 2 and 3 to determine the natural cubic interpolant S(x) and the derivative S
0
(x) for a set of experimental data that is
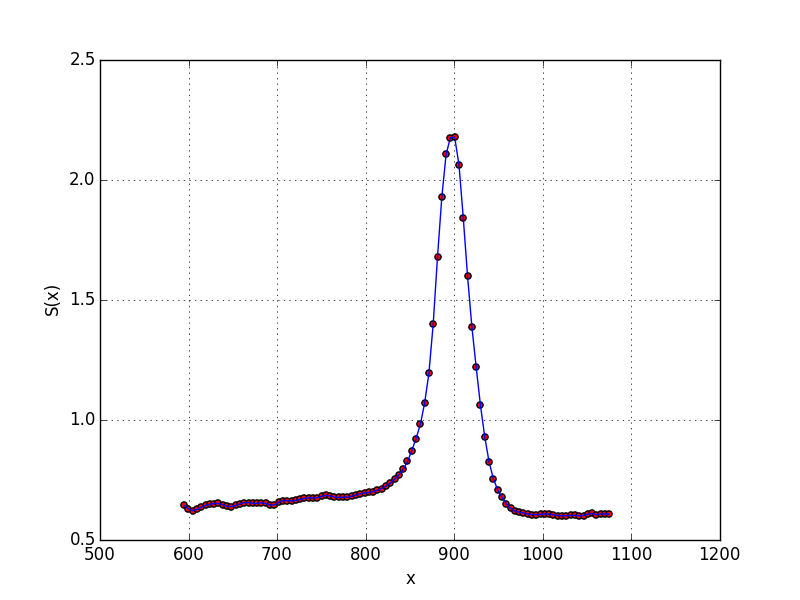
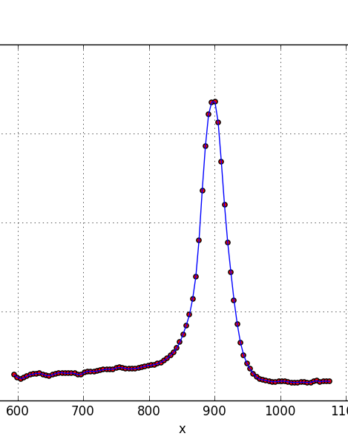
available in MyCourses (titanium.dat).
Present your results graphically (plot of S(x) vs. x and S
0
(x) vs. x).
(b) (MATLAB) Examine what functions can be found in the Matlab Spline toolbox. Repeat part (a) using Matlab functions. Compare the results. Are there differences? What is
causing them?
1